Evaluate the following iterated integral – As we embark on the evaluation of iterated integrals, we enter a realm where the significance of integration takes center stage. Iterated integrals, the repeated integration of functions over multiple dimensions, play a pivotal role in various scientific and engineering disciplines, offering a powerful tool for solving complex problems.
Delving into the intricacies of iterated integrals, we will explore the fundamental methods employed for their evaluation, including Fubini’s Theorem, change of variables, and integration by parts. These techniques provide a systematic approach to breaking down complex integrals into manageable components, enabling us to determine their values with precision.
Iterated Integrals
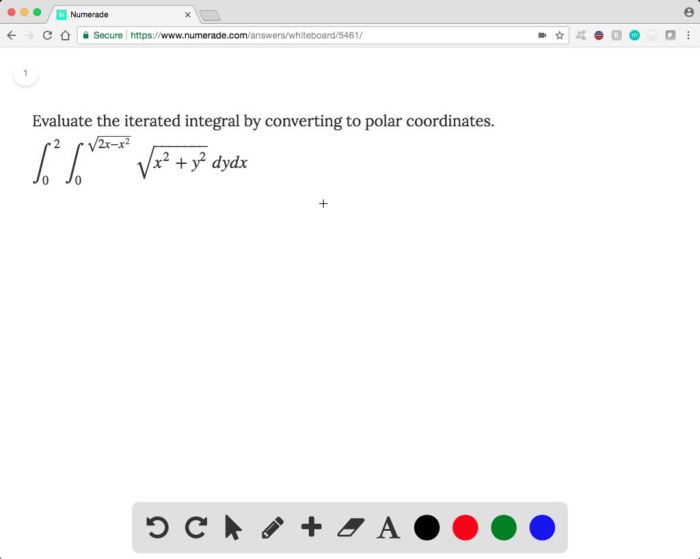
An iterated integral is a multiple integral that is evaluated by integrating one variable at a time. It is often used to calculate the volume of a solid or the surface area of a surface.
To evaluate an iterated integral, we start by integrating the innermost integral with respect to the innermost variable. We then substitute the result of this integration into the next innermost integral and integrate with respect to the next innermost variable.
We continue this process until we have evaluated all of the integrals.
Methods of Evaluation, Evaluate the following iterated integral
There are several different methods for evaluating iterated integrals. The most common methods are:
- Fubini’s Theorem
- Change of Variables
- Integration by Parts
Fubini’s Theorem
Fubini’s Theorem states that the iterated integral of a function over a region can be evaluated by integrating the function with respect to one variable at a time.
In other words, we can evaluate the iterated integral
$$\int_a^b \int_c^d f(x, y) \ dx \ dy$$
by first integrating with respect to x:
$$\int_a^b \left(\int_c^d f(x, y) \ dx\right) \ dy$$
and then integrating with respect to y:
$$\int_a^b \left[\int_c^d f(x, y) \ dx\right] \ dy$$
Change of Variables
The change of variables method can be used to evaluate iterated integrals over regions that are not rectangular.
To use the change of variables method, we first find a new set of variables that will make the region of integration rectangular. We then substitute the new variables into the iterated integral and evaluate the integral.
Integration by Parts
The integration by parts method can be used to evaluate iterated integrals that contain products of functions.
To use the integration by parts method, we first choose one of the functions in the product to be the “u” function and the other function to be the “dv” function. We then integrate by parts to get the following formula:
$$\int u \ dv = uv
\int v \ du$$
We can then use this formula to evaluate the iterated integral.
Applications
Iterated integrals have a wide range of applications in mathematics and physics. Some of the most common applications include:
- Calculating the volume of a solid
- Finding the surface area of a surface
- Evaluating probabilities
Calculating the Volume of a Solid
The volume of a solid can be calculated by integrating the cross-sectional area of the solid with respect to the height of the solid.
For example, the volume of the solid bounded by the planes x = 0, x = 1, y = 0, and y = x can be calculated by integrating the cross-sectional area of the solid with respect to x:
$$\textVolume = \int_0^1 \left(\int_0^x 1 \ dy\right) \ dx$$
Finding the Surface Area of a Surface
The surface area of a surface can be calculated by integrating the surface area element of the surface with respect to the surface area parameters.
For example, the surface area of the surface z = x^2 + y^2 can be calculated by integrating the surface area element of the surface with respect to x and y:
$$\textSurface Area = \int_0^1 \int_0^1 \sqrt1 + (2x)^2 + (2y)^2 \ dx \ dy$$
Evaluating Probabilities
Iterated integrals can be used to evaluate probabilities.
For example, the probability that a random variable X takes on a value between a and b can be calculated by integrating the probability density function of X with respect to x:
$$P(a < X < b) = \int_a^b f(x) \ dx$$
Questions and Answers: Evaluate The Following Iterated Integral
What is the significance of iterated integrals?
Iterated integrals provide a means to calculate volumes, surface areas, and probabilities, making them indispensable in various scientific and engineering applications.
What are the different methods for evaluating iterated integrals?
Common methods include Fubini’s Theorem, change of variables, and integration by parts, each offering a systematic approach to simplifying complex integrals.
How are iterated integrals used in real-world applications?
Iterated integrals are employed in fields such as physics, engineering, and economics to solve problems involving volumes, surface areas, and probabilities.




